0と1について物理的に考えてみる:続

前回に引き続き0と1について真剣に物理的に考えます。

おさらい

1と0はスイッチのONとOFFで表現し、1バイトはスイッチ8つで出来ているみたいな話をしました。
そんなスイッチを制御しているコンピュータの構成から何故か電気とは何かを話始めました。
電気の正体は電荷であり、電荷が影響する空間が電界でした。
そんな電界の中に置かれた電荷が持つ位置エネルギーのことが電位で、ある点とある点の電位の差が電位差・電圧というところまでいきましたね。

本当はこんな電気の話するつもりはなかったのですが、テンション上がってしまったのでやり切ります。

今まで電荷という粒が1粒、2粒の世界を考えてきました。でも1粒とか2粒の電荷だけで電気機器は動きません。

今回は電流についてと導体と大量の電荷について考えます。
導体ってのは電気の通しやすい物質のことで、銅とか鉄のような金属のことだと思ってください。

電流って何だ？

聞いたことあるでしょう。単位はアンペア[A]です。
こいつの正体は電荷の移動（流れ）です。「1秒間に流れる電荷の量」を電流と呼びます。

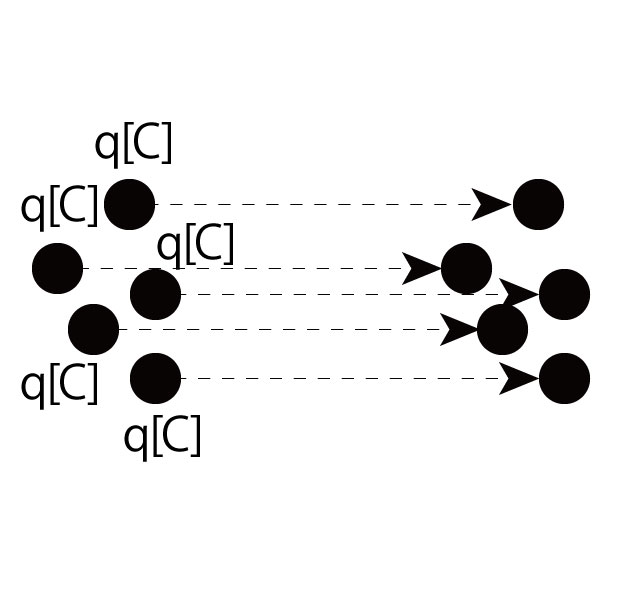
5個のq[C]が1秒間に移動したら5q[A]になります。
この電荷が電子だったら、電子はe=1.6×10^-19[C]なので、
5×e = 5×1.6×10^-19 = 8×10^-19[A]となります。少な！

電力会社との契約で20[A]とかあるじゃないですか？
20[A]が流れるってことは、20/e = 1.25×10^20個の電子が1秒間に流れてることになります。めっちゃ多いですね。10^20は日本の単位なら「垓」ですね。
1秒間にそんなに粒が流れてるんですね！

導体について考える

導体（金属）の表面に電荷がペタペタくっついた状態を帯電と言います。
マインクラフトをやっている方なら帯電クリーパーって聞いたことがあると思います。

導体の性質を一部抜粋します。

1. 導体内部の電界は0である
2. 導体内部・表面の電位は一定
3. 導体が帯電している時、電荷は内部に存在せず表面のみに分布する

1. 導体内部の電界は0であるってのは結果論でして、実際には0になるってことだと思ってます。
鉄の塊の中に複数の電荷をぶち込むと、電荷同士の反発とかで動きまわります。
その結果、自然と導体内部の電界が0になるようにそれぞれが落ち着きます。

その落ち着き先ってのが導体の表面になります。
だから3. 導体の内部に電荷が存在しないわけですね。

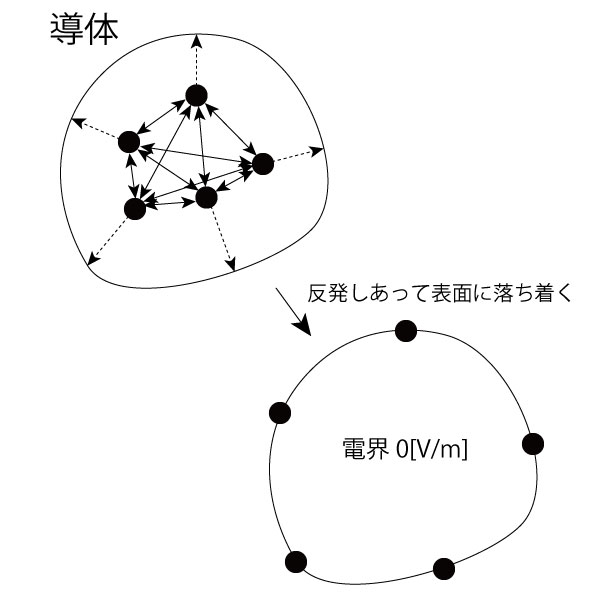
もし電荷がどこにも落ち着かずずーっと動き回っていたら、電流が発生しちゃいます。
鉄の塊の中でずーっと電流が流れちゃったら、鉄の塊はその熱でいずれ溶けちゃうかもしれませんね。

2.も簡単です。電界が0の空間では電位は変化しません。
電界の中で電荷を移動させるのに必要なエネルギーが電位なので、電界が0だったらエネルギーは0です。
なので導体表面のとある点とその反対側との間にエネルギー差はないことになります。
つまり導体表面の電位はどこでも同じになるって寸法です。

導体表面の電荷の総量をQ[C]とすると、その導体は「Q[C]で帯電している」と言います。
さらにその表面にある電荷の密度を電荷密度[C/m2]と言います。
1平方メートル当たりにある電荷の量を指します。

密度について考えてみる

前章で電荷を1粒ずつ考える時代は終わってしまいました。
何億・何兆粒・何垓粒という電子が導体内を流れているわけでして、1粒1粒について計算していては簡単に人生を使い切ってしまいます。

数学や物理学において、ものすごい大量のものを扱う際には密度を使用します。
1つ1つでなくある程度の塊で考えた方が楽ですからね！
例えば、私たちの体でも骨密度とか聞いたことあるでしょ？
スッカスカの骨なら密度が小さいし、超健康ガッチガチの骨なら骨密度が大きいってわけです。

電気の世界で使う密度は先ほどの電荷密度の他に、電流密度や電束密度などが存在します。

最初に密度って概念を考えた人は偉いですよねー。

導体と導体

ここにQ[C]で帯電した導体Aがあります。
そこに帯電していない導体Bをくっつけます。
くっついた瞬間に2つの導体は1つの導体とみなされます。

よって導体A+Bが爆誕したわけです。
この時、導体Aが持っていた電荷は導体Bの方にも移動します。

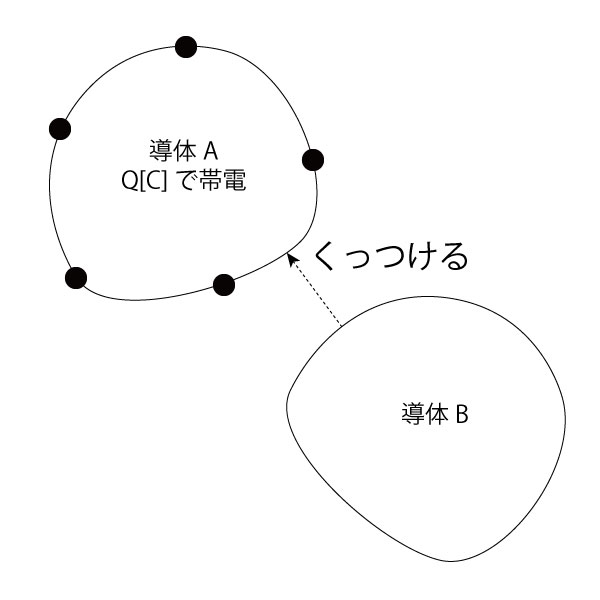
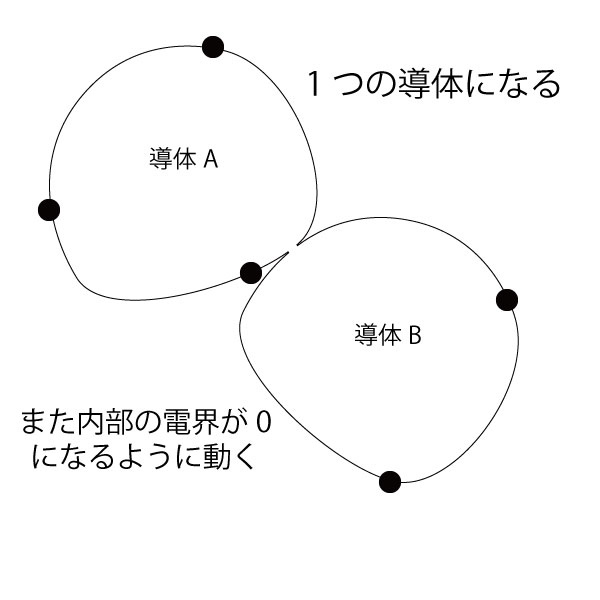
これにて導体A+BはQ[C]で帯電したことになります。
表面積が増えたことにより電荷密度は下がりましたが、導体A+Bは同電位になりました。

これが電気回路の基礎中の基礎になります。

電気回路って何だ？

みなさんも電池で豆電球を光らせたことがあるでしょう。

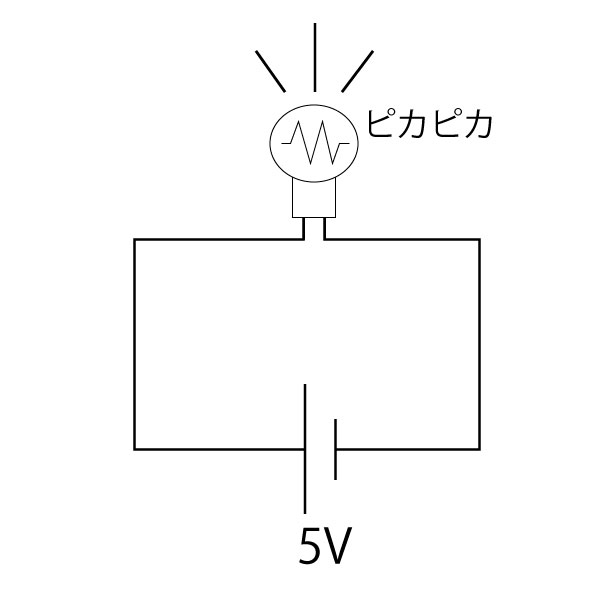
上図が電気回路です。なんで光るの？って思いません？
ってか電池って何？って思いますよね。

電池って何だ？

電離（イオン化）と言う小難しい現象が関係しています。電解液と呼ばれる液体に2種類の金属を沈めると起こる現象です。化学も関わってきてメチャメチャムズイです。実は化学苦手なんです。

簡単なモノだとレモン（クエン酸）に銅板と亜鉛版をぶっ刺すだけで電池になります。

詳しい話は飛ばすと電離によって2種類の金属の間に電位差が発生するのです。

イメージしやすい電池解説

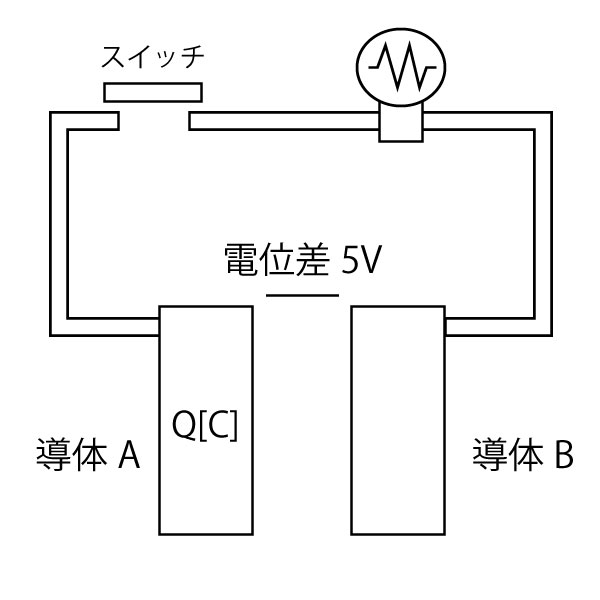
2種類の金属を導体A・導体Bとしましょう。
それらを繋ぐ電線も導体です。スイッチも導体です。豆電球は電流が流れると熱くなって光る導体です。
つまりここに描いたものは全て導体です。

この導体たちのうち同電位のものを挙げます。

• 導体Aとスイッチ左側の電線
• スイッチ右側の電線と豆電球の両端、豆電球右側の電線と導体B

ここからはイメージのしやすさのためのフィクションです。
何となくそれっぽいだけで全然違いますのでお気をつけを。
正しい解説を知りたい方は是非ともご自身で調べていただきたい！

導体Bは受け取った電荷を電解液に逃しちゃうと考えてください。
だからスイッチを入れて全てが1つの導体になったとしても導体Bは帯電しない導体です。
帯電した導体Aと帯電していない導体が電線とスイッチを経由してくっついている限り、電荷は移動します。
導体Aが持ってる電荷を全て導体Bが電解液に逃すまで電荷を流し続けるわけです。
こんな導体Aと導体Bのセットを電池と呼びます。

ちょっと難しいそこそこ本当の電池解説

導体Aから導体Bにプラスの電荷が移動するのでなく、導体Bから導体Aに電子（マイナスの電荷）が移動します。
マイナスが右から左に行くのは、プラスが左から右に移動するのと変わらないのです。

導体Bは電解液に溶ける時にいくつか電子を手放します。
手放した電子は導体Bに残り、導体Bはマイナスの電荷で帯電します。
導体Aはあまり溶けませんが、電解液中の電子を欲しがってる子に渡します。
導体Aは電子（マイナスの電荷）を手放すので、相対的にプラスの電荷で帯電します。

導体Bは電子が余る。導体Aは電子を電解液中に渡す。互いの利益が一致するので、スイッチがONなら電子は導体Bから導体Aに流れるわけです。
この利害関係で成り立つ2種類の金属および電解液のセットを電池と呼びます。

化学が苦手なのでこれが限界です。。。

スイッチの進化

これである程度簡単な電気回路の仕組みがわかりました。
それではスイッチの進化についてお話ししましょう。
さきほどの電気回路で出てきたスイッチはポチッと手で押すタイプでした。

導体の接触を物理的に制御していたわけでして、単純かつ確実に電流の移動を制御できます。

先週の序盤で1GBはスイッチ80億個で成り立っているとお話ししたかと思います。
コンピュータは80億個のスイッチを頑張ってポチポチしているの？と不安になったでしょう。

大丈夫です。さすがに物理接触によるスイッチではありません。
使われているのはトランジスタと呼ばれるスイッチです。
コンピュータで使われるスイッチが全てトランジスタってわけではありませんが、スイッチの代表例であることは間違いないです。

トランジスタって何だ？

トランジスタは半導体で出来ています。
今まで導体は何度も出てきたけど、半導体？半分導体ってこと？と思うでしょう？

その通りです。半分導体なんです。

半導体って何だ？

半導体は、電流が流れやすいとも電流が流れずらいとも言える物質のことです。
金属のような導体は電流が流れやすいもののことでしたね。
ちなみに電流の流れやすさを電気伝導度と呼びます。

半導体として有名なのはシリコンですね。
完全に純粋なシリコンの塊は真性半導体って言ってほぼ電気を通しません。

だから別の物質を混ぜることで電流の流れやすさを調節するのです。

電流が流れやすいってどういうことだ？

電流は電荷の移動のため、電荷が移動しやすいとも言い換えられますね。
物質の電荷ってのは電子のことですので、電子の移動のしやすさと言えますね。

普通、電子は原子核の周りをグルグル回っています。原子核に束縛されているとも言えます。
でも誰にも束縛されない自由な電子が存在します。その名も自由電子です。
導体っていうのはこの自由電子がたくさんあるものを指します。
これに電界を与えた場合に電子は電界によって移動します。これが電気伝導と呼び、その量が電流というわけです。

電気伝導度あるいは電気伝導率はコンダクタンスとも呼ばれます。
私は英語が好きなのでこれからコンダクタンスと呼ぶことにします。

余談ですが流れやすさの反対である、流れずらさを電気抵抗率と呼びます。
オームの法則の抵抗はコレに関係しています。

物質によってコンダクタンスが決まっています。
金属はコンダクタンスが大きいってわけですね。

で、半導体って何だ？

シリコンに混ぜる物質によって半導体は

• n型半導体
• p型半導体

に分かれます。
物質ってのは色んなくっつき方をします。
その中に共有結合と呼ばれるくっつき方をするものがあるのです。
隣り合った原子同士がお互いの電子を共有することで安定する結合です。

例えばシリコンは4つの電子を持っていて、あと4つ欲しがっています。
それらがお互いの電子を共有することでその欲望をかなえるわけです。
以下の図を見ればめっちゃわかると思います。

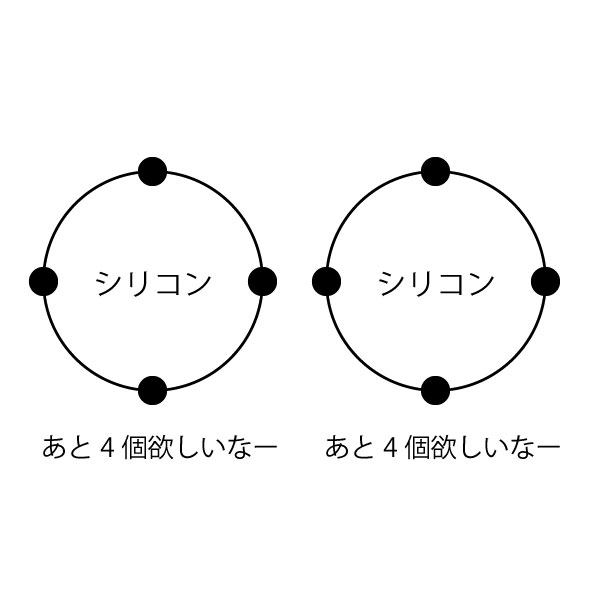
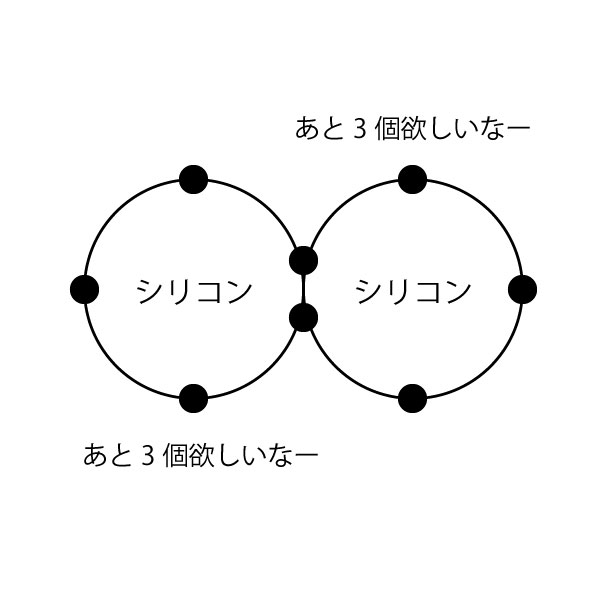
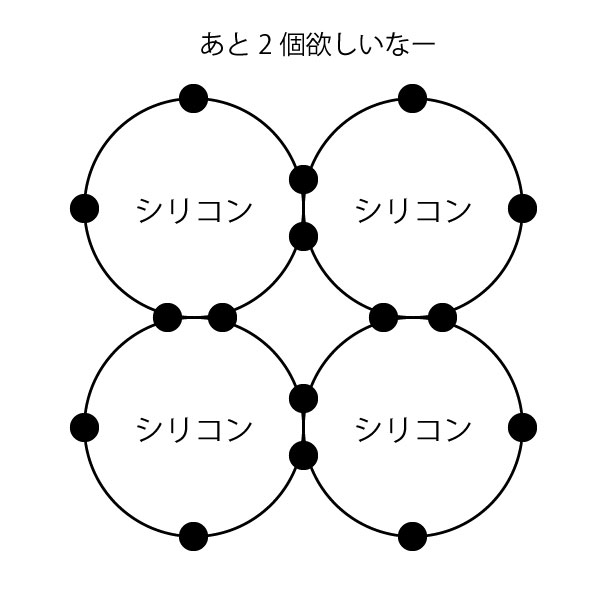
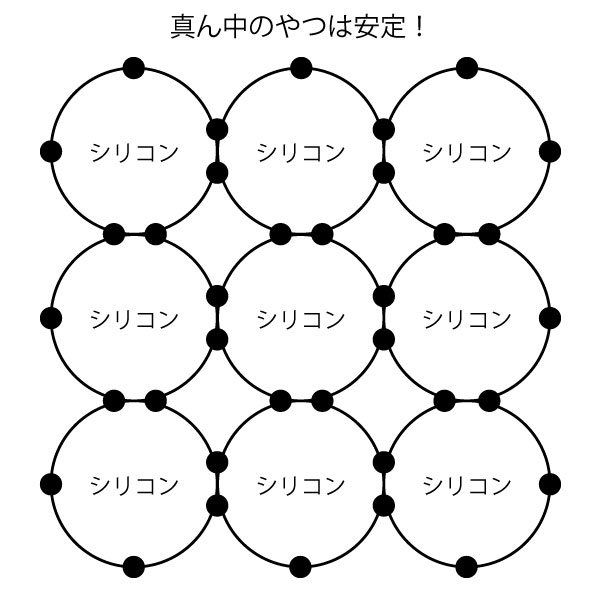
ってことです。

最後の図では中央は安定してます（欲望を叶えてます）。
でも四隅は2つの電子がフワフワしてます。上下左右の電子は1つの電子がフワフワしているわけです。
こういうフワフワした電子が自由電子になりやすいんです。

こんなシリコン結晶に電子余してます！ってのを注入したり、電子全然足りてないです！ってのを混ぜると自由電子が増えたり、逆に電子の穴（ホール）ができたりします。

電子が増えて自由電子が多くなった半導体をn型半導体と呼びます。
nはネガティブのnです。電子はマイナスの電荷なので全体的にマイナスつまりネガティブだということです。
逆に電子が足りなくて電子の穴（ホール）が多い半導体をp型半導体と呼びます。
pはポジティブのpです。電子の穴（ホール）は相対的にプラスの電荷と見れるのでポジティブってことですね。

ちなみにこの自由電子やホールのことをキャリアと呼びます。

p型とn型があるのはわかったけどだから何なん？

p型とn型の半導体をくっつけると、こんなものが作れます。

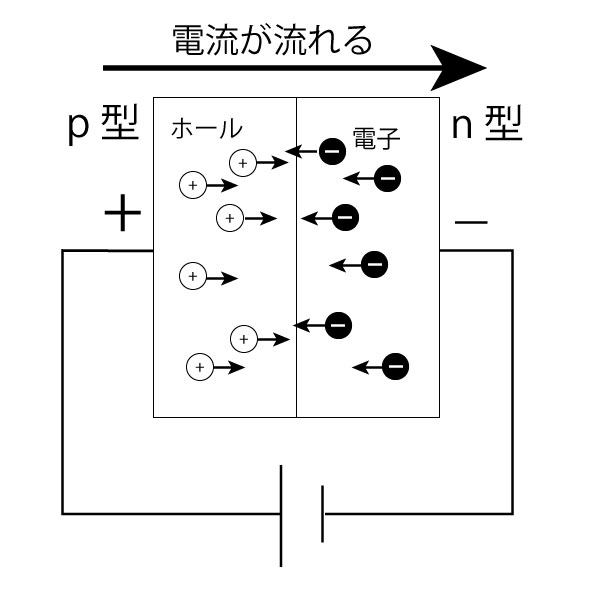
これはpn接合ダイオードって言います。
p側の電位が高いとホールは反発してn側に移動。逆にn型から電子を引き寄せます。プラスが左から右、マイナスが右から左に移動するってことは全体が右に流れていることになります。

でも逆電圧をかけると、電流は絶対に流れません。要は電流の一方通行路なわけですね。
電流の逆流を防ぐのに使われますね。

こんな感じでp型とn型は組み合わせて色々作れます。

トランジスタを作る

原理が簡単なトランジスタにnpn型バイポーラトランジスタとpnp型バイポーラトランジスタがあります。

npn型バイポーラトランジスタについて説明しますね。
バイポーラトランジスタってのはバイ（2つ）ポーラ（極）トランジスタって意味です。2つの極ってのが電子とホールのことです。

npnと書いている通りp型をn型でサンドイッチします。

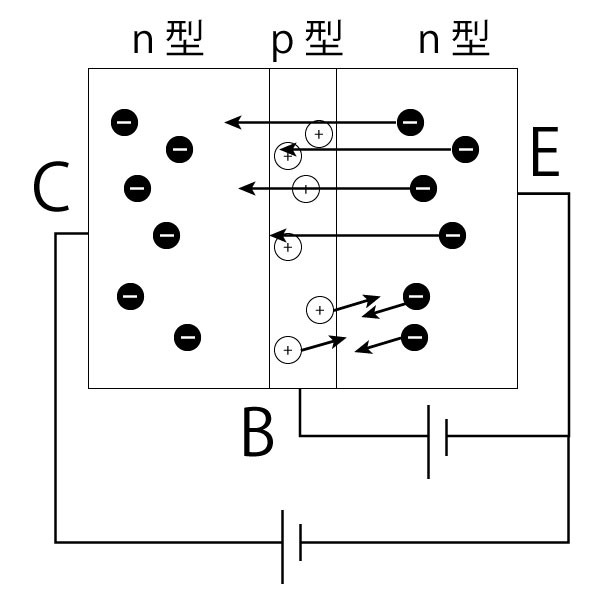
真ん中のp型はめっちゃ薄いものをくっつけます。

左のn型がコレクタ（C）という端子につながっており、真ん中のp型はベース（B）、右のn型がエミッタ（E）という端子につながっています。

ベース・エミッタ間に電圧をかけると、ベースからエミッタに少量の電流が流れます。これはエミッタからベースに向かって電子が移動するからです。
ベースはめちゃくちゃ薄いので、エミッタからの電子は勢い余ってベースを通り越しちゃいます。
そうすると、コレクタのプラス電圧によってその電子はコレクタ端子にたどり着きます。

ベースからエミッタに流す電流（ベース電流）が少なければ、エミッタからコレクタに勢い余って行く電子（コレクタ電流）は少なくなります。
つまり、ベース電流でコレクタ電流を制御できるわけです。

要はトランジスタはベース電流を流せばON（C-E間が導通）、流さなければOFF（C-E間が断絶）のスイッチとして使えるということですよ！

コンピュータの話に戻る

コンピュータなんてトランジスタの塊みたいなもんです。
もちろんダイオードも使われてますし、もっとよくわからない素子もたくさん使われています。
コンピュータに限らずあらゆる電化製品に欠かせない素子であることに間違いありません。

0と1について物理的に考えてみる

0と1はスイッチのON・OFFで表現できます。
そのスイッチとはポチポチ押すスイッチでなく、電気で電気をON・OFFするトランジスタです。
ちなみにトランジスタによる0と1表現はメモリやレジスタなんかでたくさん使われているようです。電気を止めると一度全てなかったことになったりします。

もちろん他にも0と1を表すものはあります。
磁気記憶装置ではS極とN極の並びで0と1を表現します。これは電気を止めてもその並びは変わらないからハードディスクやフラッシュメモリで使われます。

どうです？この言葉達が今のあなたならほぼほぼ理解できるのではないでしょうか？

終わりに

長かったですねー。お疲れ様でしたー。
学生の頃と前職の頃に蓄えた知識がまさかこんなところで披露されるとは思いもよらなかったです。
是非ともみなさんも深淵なる電気の世界に足を踏み入れてはいかが？
この世界を動かす多数の法則と出会えるチャンスが目の前にありますよ！

それではまた来週！
来週はプログラムのことを書きたい！